2 calculs de différentielles – Casio GRAPH 35+ Manuel d'utilisation
Page 85
55
3-2 Calculs de différentielles
[OPTN]-[CALC]-[d/dx]
Pour effectuer des calculs de différentielles, affichez d’abord le menu d’analyse
de fonctions, puis entrez les valeurs indiquées dans la formule suivante.
2(
d
/
dx
)
f(x)
,
a
,
A
x
)
La différentiation pour ce type de calcul est définie en tant que :
Dans cette définition,
infinitésimal est remplacé par suffisamment petit A
x
, avec
la valeur aux environs de f ' (a) calculée en tant que :
Afin d’apporter la meilleure précision possible, la machine emploie la différence
moyenne pour réaliser les calculs différentiels. L’exemple suivant illustre la
différence moyenne.
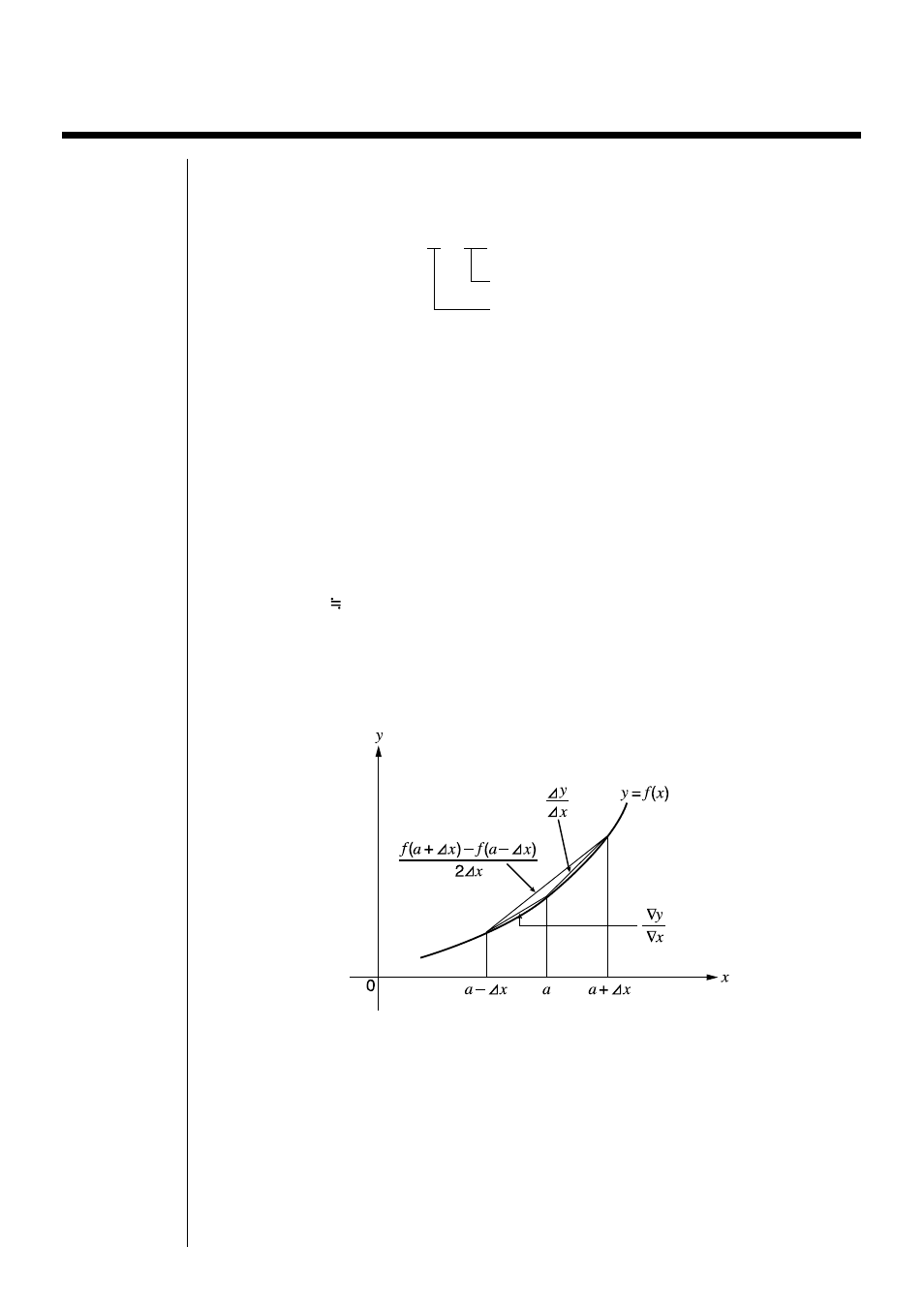
Les pentes des points
a
et
a +
A
x
, et des points
a
et
a –
A
x
dans la fonction
y = f(x)
sont les suivantes :
Dans l’exemple ci-dessus, A
y
/A
x
est appelé la différence avant, tandis que ∇
y
/∇
x
est la différence arrière. Pour calculer les dérivées, la machine prend la
moyenne entre les valeurs de A
y
/A
x
et ∇
y
/∇
x
, apportant ainsi une plus grande
précision pour les dérivées.
d
d/dx ( f (x), a, A x)
⇒ ––– f (a)
dx
Accroissement/décroissement de
x
Point pour lequel la dérivée doit être déterminée
f (a + Ax) – f (a)
f '(a) = lim –––––––––––––
Ax
Ax→0
f (a + Ax) – f (a)
f '(a) –––––––––––––
Ax
f (a + Ax) – f (a)
A
y
f (a) – f (a – Ax)
∇
y
––––––––––––– = ––– , ––––––––––––– = –––
Ax
Ax
Ax
∇x