Casio GRAPH 85 - Manuel (Page 110)

20050301
2-6-3
Calculs avec nombres complexes
k k k k k Valeur absolue (module) et argument
[OPTN]-[CPLX]-[Abs]/[Arg]
La machine considère un nombre complexe dans la forme Z = a + bi comme des
coordonnées sur un plan de Gauss et calcule la valeur absolue Z et l’argument (arg).
○ ○ ○ ○ ○
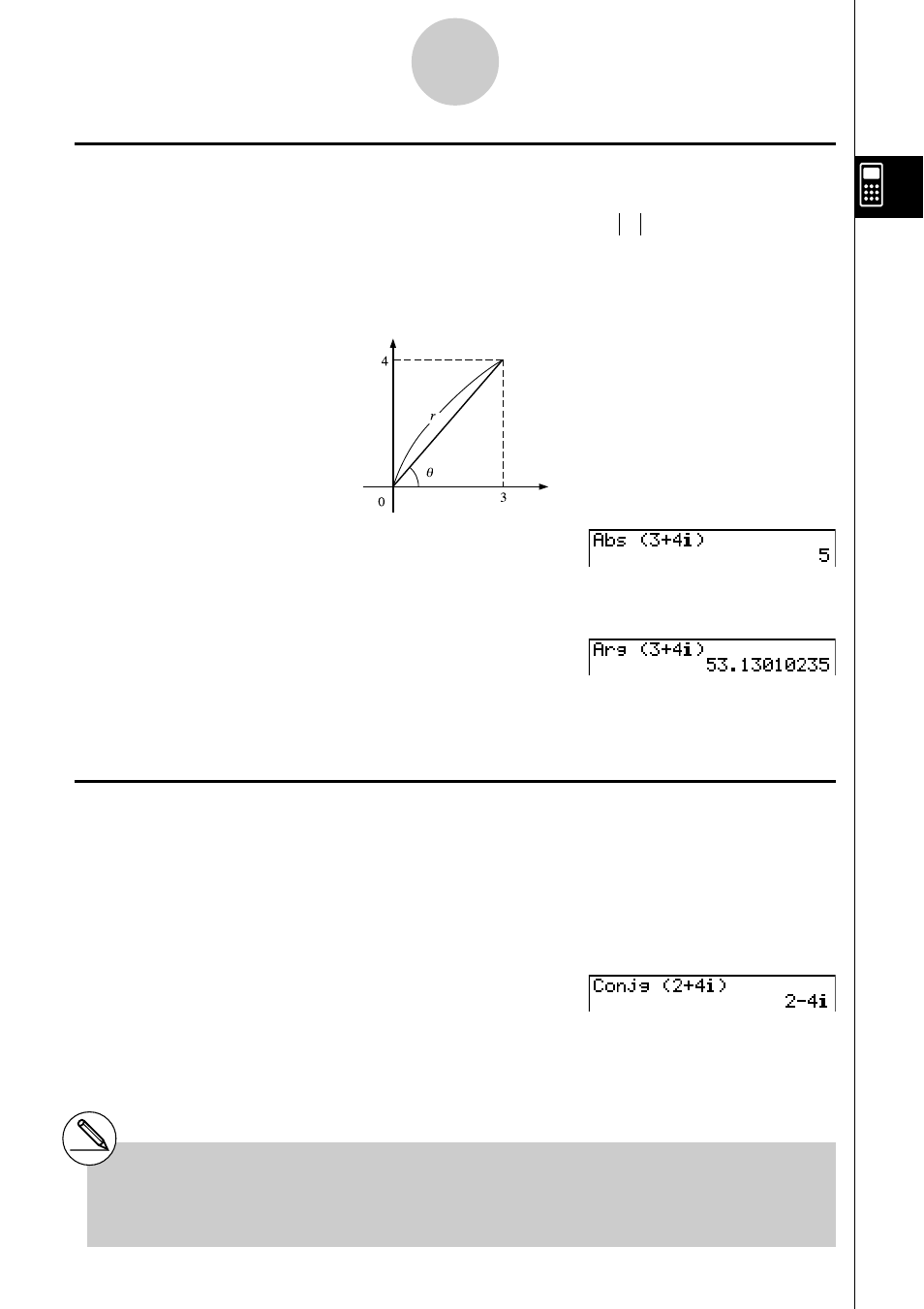
Exemple Calculer la valeur absolue ( r ) et l’argument (
θ) du nombre complexe
3 + 4 i , avec le degré comme unité d’angle
AK3(CPLX)2(Abs)
(d+e 1( i ))w
(Calcul de la valeur absolue)
AK3(CPLX)3(Arg)
(d+e 1( i ))w
(Calcul de l’argument)
k k k k k Nombres complexes conjugués
[OPTN]-[CPLX]-[Conj]
Un nombre complexe de format a + bi devient un nombre complexe conjugué de format
a – bi .
○ ○ ○ ○ ○
Exemple Calculer le nombre complexe conjugué pour le nombre complexe
2 + 4
i
AK3(CPLX)4(Conj)
(c+e 1( i ))w
# Le résultat du calcul de l’argument change
selon l’unité d’angle (degré, radian, grade)
sélectionnée.
Axe imaginaire
Axe réel